2009年408数据结构程序设计题

题目

（15分）已知一个带有表头结点的单链表，结点结构为：

假设该链表只给出了头指针list。在不改变链表的前提下，请设计一个尽可能高效的算法：
查找链表中倒数第 k 个位置上的结点(k 为正整数)。
若查找成功，算法输出该结点的 data 域的值，并返回 1；否则，只返回 0。
要求：
⑴ 描述算法的基本设计思想；
⑵ 描述算法的详细实现步骤；
⑶ 根据设计思想和实现步骤，采用程序设计语言描述算法

注意题目所给信息
1.带头结点
2.单链表：不能访问前继节点，只能访问后继节点。
3.未知单链表长度
4.k为正整数，即k>0。不需要做k<=0越界判断。

单链表

单链表（单向链表）数据结构回顾：
单链表是线性表的链式存储。由多个节点组成，每个节点又由数据域和指针域构成。如图：

结点结构

用一个结构体描述节点类型：

struct ListNode {
  int data;  //节点的数据域，用来存放数值内容 
  struct ListNode *link;  // 节点的指针域，用来指向下一个节点 
};

这里的节点结构内容和题目所给的一致。

头节点

关于头节点一些需要的注意的，做出如下总结梳理
说明：
1.头节点不是链表第一个节点，而是头节点随后紧邻的后继节点。
2.头节点是非必须的，可以不设置。
3.在计算链表长度时，头节点不计入总数。
4.头节点的数据域没有意义。

好处：
1.使链表首个位置的插入删除更加方便，和其他位置一样，不需要涉及到头指针的移动。
2.统一空表和非空表的操作处理。当非空时头指针指向的是首个节点的地址，即*ListNode类型，而对空表处理的时候却是NULL，因此造成空表和非空表操作不一致。

头指针

其实指向某个节点的地址的指针丢失，也会造成这个节点无法访问。特别是头指针，一旦丢失，导致链表最前面的节点（头节点或者是第一个节点）无法访问，从而导致整个链表无法访问，出现内存泄漏等问题。
作用：具有标识作用，故常用头指针冠以链表的名字

单链表基本操作

链表的基本操作如下：

链表的初始化

/*
单链表的初始化
返回一个ListNode指针类型变量，即链表的头指针
*/
struct ListNode* initLinkList(){
  struct ListNode *head;  //定义头节点
  head = (struct ListNode *)malloc(sizeof(struct ListNode));  //头结点空间申请
  //这里做一个判断，判断头节点是否申请成功
  if(head == NULL){
    printf("内存不足！申请内存空间失败\n");
  }
  head->link = NULL;  //头节点指向的下一个节点位置置为空
  return head;  //返回头节点地址
}

节点的创建

将创建新节点这个过程封装到一个函数，便于复用。

/*
新创建节点
返回值：新节点地址
*/
struct ListNode* newNode(int data, struct ListNode *link){
  struct ListNode *newNode;  //定义新节点
  newNode = (struct ListNode*)malloc(sizeof(struct ListNode));  //新结点空间申请
  newNode->data = data;  //新结点数据域初始化
  newNode->link = link;  //新结点指针域初始化
  return newNode;
}

节点的插入

思路：
调用findNodeByIndex函数(查找节点操作)，获得第 i-1 节点，然后再进行插入操作。

具体的原理实现如下图所示：

说明：
这里一个数值，以及新节点所在位置来实现单链表中新节点插入操作。
新节点创建在函数内进行，并不是通过真正意义上传入一个节点类型实现插入操作。
时间性能：O(n)

具体步骤：

1. 首先需要找到插入位置的前一个节点, 也就是图上节点preNode。若找不到，则是越界等问题，返回报错信息。
2. 然后需要创建新的节点newNode。
3. 插入操作实际上就是把preNode的后继节点改为新节点newNode，然后再把新节点newNode的后继节点改为第 i节点。需要注意顺序，以防出现断链。改动指针操作顺序正如图所示，先①后②。
   代码如下：
   ①：newNode->link = preNode->link;
   ②：preNode->link = newNode;
   对于①表示把新节点newNode的后继节点改为第 i节点。第 i节点的地址通过它的前继节点来寻找，即：preNode->link
   对于②表示把preNode的后继节点改为新节点newNode

/*
插入节点操作
list*：新节点插入所在的链表
index：新节点插入的位置
data：新节点数据域的值
返回值：
0：插入失败
1：插入成功
*/
int addNodeByIndex(struct ListNode *list, int index, int data){
  /*
  判断说明：
  这里需要注意边界问题，当传入参数index=1时，
  也就是带头单链表插入的位置是第1个节点的位置，既然知道了位置
  下面无需调用findNodeByIndex函数
  */
  if(index == 1 || list->link == NULL){
    list->link = newNode(data, list->link);
    return 1;
  }
  struct ListNode *preNode;  //定义插入节点的前一个节点
  preNode = findNodeByIndex(list, index - 1);  //查找前一个节点是否存在
  if(preNode == NULL){
    printf("插入失败, 位置越界！\n");
    return 0;
  }
  preNode->link = newNode(data, preNode->link);
  return 1;
}

节点的删除

原理如图：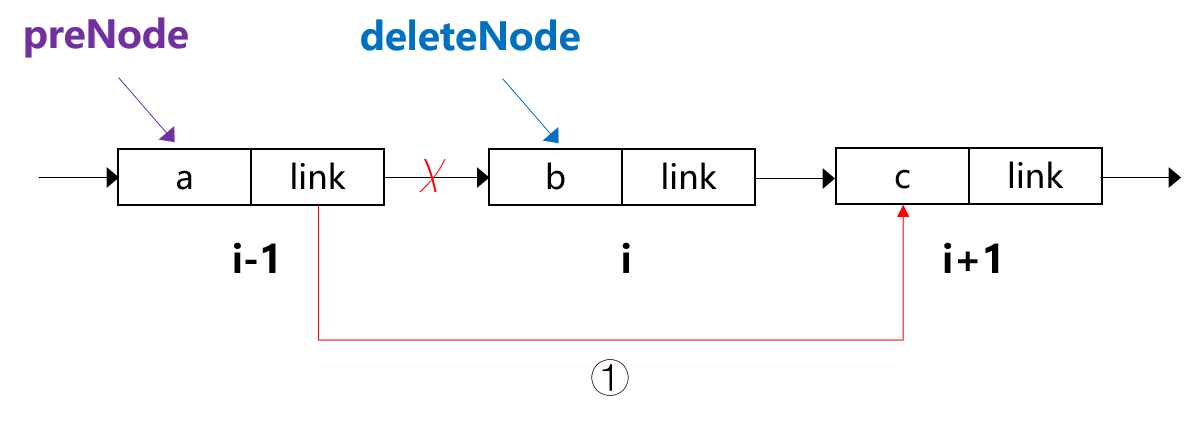

思路：
调用find方法(查找节点操作)，获得第 i-1 节点，然后再让 i-1 位置节点的指针域指向 i 位置节点后继节点。
时间性能：O(n)
注意：先修改指针再释放节点，避免断链。
代码如下：

/*
通过位置删除节点操作
list*：需要删除节点所在的链表
index：需要删除节点的位置
返回值：
0：删除失败
1：删除成功
*/
int deleteNodeByIndex(struct ListNode *list, int index){
  
  struct ListNode *preNode;  //需要删除节点的前一个节点
  struct ListNode *deleteNode;  //需要删除的节点

  /*
  判断说明：
  这里需要注意边界问题，当传入参数index=1时，
  也就是删除单链表第一个节点，此次就要注意index-1<=0,
  下面调用findNodeByIndex()函数会提示越界异常错误, 得到空指针。
  */
  if(index == 1){
    preNode = list;
    deleteNode = list->link;
  }else{
    preNode = findNodeByIndex(list, index - 1);  //查找前一个节点是否存在
    
    /*
    参数 index < 1 的时候，下面调用findNodeByIndex()函数会提示越界异常错误, 得到空指针。
    此时index - 1 作为参数依然小于1, 调用findNodeByIndex()函数会提示越界异常错误, 得到空指针。
    如果参数大于链表长度，例如链表长度为3，而index传入参数的值为4的时候，显然会越界，但是index-1=3，
    链表确实有第3个节点，因此加上判断条件preNode->link==NULL就可以实现越界判读。
    */
    if(preNode == NULL || preNode->link==NULL){
      printf("删除失败, 位置越界！\n");
      return 0;
    }
    deleteNode = preNode->link;
  }
  /*
  printf("preNode：%d\n", preNode);
  printf("deleteNode：%d", deleteNode);
  */
  preNode->link = preNode->link->link;
  free(deleteNode);  //释放要删除结点的内存空间
  return 1;
}

节点的修改

思路：
调用find方法(查找节点操作)，然后再进行修改操作。
时间性能O(n)

/*
通过节点位置来修改节点数据域操作
list*：需要修改节点所在的链表
index：需要修改节点的位置
data：需要修改节点数据域的值
返回值：
0：修改失败
1：修改成功
*/
int updateNodeByIndex(struct ListNode *list, int index, int data){
  struct ListNode *updateNode;
  updateNode = findNodeByIndex(list, index); //查找需要修改的节点是否存在
  if(updateNode == NULL){
    printf("修改失败, 位置越界！\n");
    return 0;
  }
  updateNode->data = data;
  return 1;
}

节点的查找

思路：
插入前需要进行合法性判断，例如插入位置是 -1 或者是超过表长时，显然不合法。
位置合法以后，因为单链表中每个节点的查找都通过它的前继节点来访问，因此进行逐一遍历查找。
时间性能：O(n)

/*
根据给定位置来查找链表中该位置的节点
list*：需要查找节点的所在链表
index：需要查找节点的位置
返回值：该位置节点的地址
*/
struct ListNode* findNodeByIndex(struct ListNode *list, int index){
  //检查位置合法性
  if(index <= 0){
    printf("节点位置异常, 不能为负数\n");
    return NULL;
  }
  int len = getLinkLength(list);
  if(index > len){
    printf("节点位置异常, 位置超出表长\n");
    return NULL;
  }

  int i = 0;
  struct ListNode *p;
  p = list;
  
  while(i != index){
    p = p->link;
    i++;
  }
  return p;
}

求链表长度

思路：
设置一个计数器，然后逐一遍历节点，每经过一个节点计数器+1。
时间性能：O(n)

/*
求带头结点的单链表的表长
返回值：单链表的长度
*/
int getLinkLength(struct ListNode *list){
  int len = 0;
  struct ListNode *p;
  p = list;
  while(p->link != NULL){
    p = p->link;
    len++;
  }
  return len;
}

打印单链表

打印链表信息，输出每个节点地址，指向的下一个节点，内容以及表长。
时间性能：O(n)

void printfLink(struct ListNode *list){
  int len = 0;  //表长计数
  struct ListNode *p;
  p = list;
  printf("头节点地址：%d\n", p);
  while(p->link != NULL){
    p = p->link;
    len++;
    printf("第%d个节点地址：%d\t数据域内容：%d\t指针域指向地址：%d\n", len, p, p->data, p->link);
  }
  printf("链表长度：%d\n", len);
}

代码的一些说明：

1. 代码为了易于初学者掌握，并没有使用typedef别名定义来简化一些复杂的类型声明。想要代码更简洁，可以去尝试一下。
2. 调用malloc()函数勿忘记头文件加上#include<stdlib.h>。
3. 测试代码如下：

   int main(){
     //定义头指针，指针变量名表示链表名称
     struct ListNode *linkList;
     //linkList的初始化
     linkList = initLinkList();
   
     //插入第1个元素，位置1
     addNodeByIndex(linkList, 1, 1);
     //插入第2个元素，位置1
     addNodeByIndex(linkList, 1, 0);
     //插入第3个元素，位置1
     addNodeByIndex(linkList, 1, 2);
     printfLink(linkList);  //输出操作结果
     //插入第4个元素，位置99
     addNodeByIndex(linkList, 99, 2);
   
     //删除位置2的元素
     deleteNodeByIndex(linkList, 2);
     printfLink(linkList);  //输出操作结果
   
     //更新位置1的元素数据域为666，
     updateNodeByIndex(linkList, 1 ,666);
     printfLink(linkList);  //输出操作结果
     return 0;
   }

4. 对于单链表的插入，删除，修改，查找都是通过位置来实现的。这四种操作还可以通过数据域进行值查找。等有时间了再补全。
5. 关于下标从0开始的问题，本程序默认第一个节点下标是1，便于理解！！如果想写成从0开始，可以直接让index参数整体-1以及边界判断条件也做小修改，整体思路不变。

题目求解

前面回顾了单链表的一些基本知识，下面来求解本题。

方法1：

蛮力法，硬算。通过多次遍历单链表，一定能求解出问题，但是时间性能得不到保障。

思路：

1.求表长len。
2.倒数第k个数，实际上就是：len-k+1，下标为len-k+1-1=len-k。
自己做个简短分析：
长度为5，倒数第5个，实际上就是第5-5+1=1个，下标为0。
长度为5，倒数第3个，实际上就是第5-3+1=3个，下标为2。
长度为5，倒数第2个，实际上就是第5-2+1=4个，下标为3。
长度为5，倒数第1个，实际上就是第5-1+1=5个，下标为4。
不难得出上面式子。
合法性判断也比较简单：倒数的数绝对超不出len的长度，如果k>len，直接返回0
3. 然后再进行遍历单链表，到达第len-n+1节点。输出data，返回1。

代码实现：

int find1(struct ListNode *list, int k){
  int len = 0;
  struct ListNode *p = list;
  
  //遍历单链表求表长
  while(p->link != NULL){
    p = p->link;
    len++;
  }
  
  //合法性判断
  if(k > len) return 0;

  int i = len - k + 1;  //拿到倒数第k的实际位置i
  p = list;  //重新初始p指针指向头节点
  
  //遍历i次，得到第i个节点
  for(i; i > 0;i--)
    p =p->data;
  
  printf("%d", p->data);  //输出倒数第k节点data值
  return 1;
}

方法2：

最优解法，一次遍历完成查询。

思路：

1.使用双指针：定义两个指针*p，*q。
2.*q指向单链表第一个节点不动，*p向后遍历k个节点。
合法性判断也比较简单：在两个指针间隔达不到k时，*p提前移动到尾结点处，则返回0
3.两个指针同时移动，直到*p移动到尾结点处。则*q指向的节点则是题目所求。

画了个图：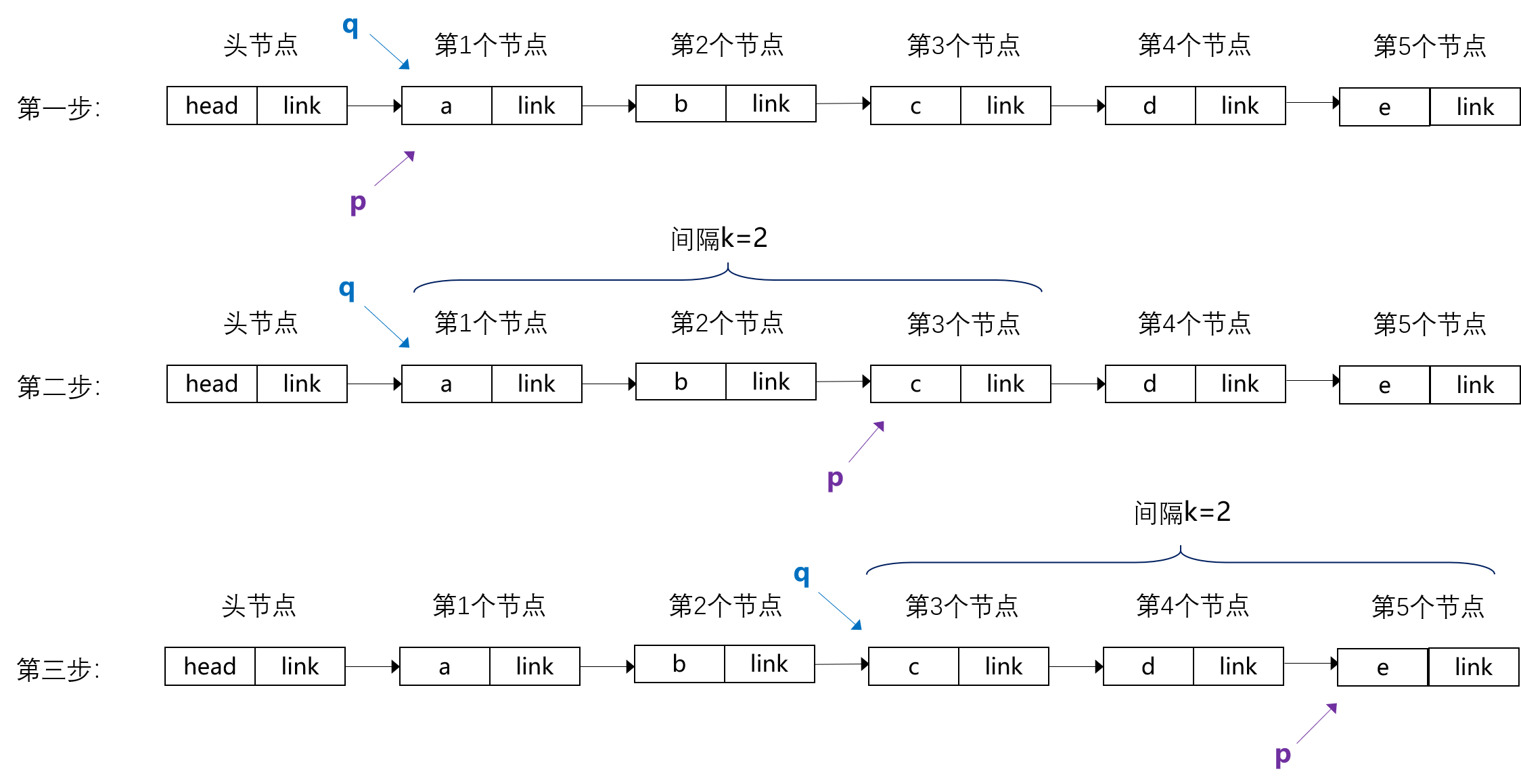

举了个例子，求倒数第2个节点的data值，最后q所指向的第3个节点是题目所求。

代码实现：

int find2(struct ListNode *list, int k){
  //初始化双指针
  struct ListNode *p = list;
  struct ListNode *q = list;
  
  int i = k;

  //p指针向前遍历k次
  while(i > 0){
    p = p->link;
    i--;
  }

  if(p == NULL) return 0;  //合法性判断

  //两个指针一起移动，直到p指针移动至表尾
  while(p != NULL){
    q = q->link;
    p = p->link;
  }
  
  printf("%d", q->data);  //输出倒数第k节点data值
  return 1;
}

本文作者： spg2021
本文链接： https://spg2021.github.io/2020/03/31/408-2009/
版权声明：文章除特别声明外，均采用 CC BY-NC-SA 3.0 许可协议。转载请注明出处！